Article Sidebar

Download
PDF
Statistic
Read Counter : 901 Download : 627

Downloads

Download data is not yet available.

Main Article Content

Abstract

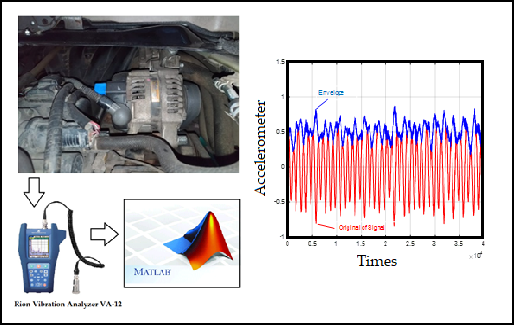
Checking the alternator with mechanical measurements of moving parts takes sufficient time, especially in compact design engines. Therefore, this article presents a new method for alternator fault detection using the Hilbert transform application. The instantaneous amplitude and frequency are used as input variables for fault detection. Joint time-frequency analysis based on the wavelet analysis is also applied to identify the nonlinear characteristics. Various wavelet functions are examined, and some recommendations regarding the most suitable ones and the interpretation of the results are discussed. As a result, the backbone curve obtained from the instantaneous amplitude and frequency demonstrates the presence of the nonlinear phenomena, which can help make decisions about an alternator in normal conditions or indicate fault detection. From the test results, this method is very promising to be applied as part of vehicle's preventive maintenance.

Keywords

Preventive maintenance Alternator Hilbert analysis Fault detection

Article Details

Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

Author Biographies

Subekti Subekti, Mercu Buana University, Indonesia

Academic profile: Scopus; ORCID; ResearchGate; Google Scholar; Sinta

Muhammad Nurul Hidayat, PT Astra Daihatsu Motor, Indonesia

Academic profile: LinkedIn

Basuki Dwi Efendi, PT Astra Daihatsu Motor, Indonesia

Academic profile: -

Abdul Hamid, Mercu Buana University, Indonesia

Academic profile: Google Scholar

Alim Murwanto, Mercu Buana University, Indonesia

Academic profile: -

References

  1. S. Subekti, “Studying The Dynamic Characteristics To Lengthen The Operating Life For A Diesel Engine Using Frequency Response Function (FRF) Measurement,” Sinergi, vol. 22, no. 3, pp. 161–168, 2018.
  2. S. Subekti, A. Hamid, B. D. Effendy, and A. W. Biantoro, “Inspecting a Bump Test in the Maintenance of a 1200-cc Daihatsu Sigra Disc Brake,” Sinergi, vol. 23, no. 3, pp. 191–198, 2019.
  3. B. D. Efendi, S. Subekti, and A. Hamid, “Karakteristik Dinamik Disc Brake Daihatsu Sigra 1200 cc dengan Metode Bump Test,” Flywheel: Jurnal Teknik Mesin Untirta, vol. 1, pp. 14–19, 2019.
  4. A. Susanto, S. Q. Yusuf, A. Hamid, H. Wahyudi, and S. Subekti, “Implementation Of Frequency Response Function On Tapper Bearing Maintenance,” Sinergi, vol. 23, no. 2, pp. 132–138, 2019.
  5. S. Subekti, A. Hammid and A. W. Biantoro, “Identifying the Nonlinearity of Structures Dynamics by Wavelet Packet Decomposition,” in IOP Conference Series: Materials Science and Engineering, 2018, vol. 453, no. 1, p. 12003.
  6. C. Tan and N. Uddin, “Hilbert transform based approach to improve extraction of‘ drive-by’ bridge frequency,” Smart Structures and Systems, vol. 25, no. 3, p. 265, 2020.
  7. A. Medoued, A. Lebaroud, and D. Sayad, “Application of Hilbert transform to fault detection in electric machines,” Advances in Difference Equations, vol. 2013, no. 1, pp. 1–7, 2013.
  8. M. Feldman, “Hilbert transform in vibration analysis,” Mechanical systems and signal processing, vol. 25, no. 3, pp. 735–802, 2011.
  9. Q. Zhou, C. Wu, and Q. Fan, “Gear Fault Diagnosis Under the Run-Up Condition Using Fractional Fourier Transform and Hilbert Transform,” in International Conference on Mechanical Design, 2019, pp. 918–943.
  10. A. Benchatti, A. D. Hammou, G. Zaza, and H. Saiah, “Fault detection method on a compressor rotor using the phase variation of the vibration signal,” International Journal of Engineering, vol. 30, no. 8, pp. 1176–1181, 2017.
  11. F. Wang and S. Duan, “Fault diagnosis of diesel engine using vibration signals,” in International Conference on Intelligent Computing and Information Science, 2011, pp. 285–290.
  12. J. Jin, I. Jung, and S.-H. Shin, “Fault Diagnosis of an Engine through Analyzing Vibration Signals on the Block,” SAE Technical Paper, 2020.
  13. H. R. E. Siller, “Non-linear modal analysis methods for engineering structures.” University of London, 2004.
  14. J. M. H. Peters, “A beginner’s guide to the Hilbert transform,” International Journal of Mathematical Education in Science and Technology, vol. 26, no. 1, pp. 89–106, 1995.
  15. M. Feldman, “Non-linear system vibration analysis using Hilbert transform--I. Free vibration analysis method’Freevib’,” Mechanical systems and signal processing, vol. 8, no. 2, pp. 119–127, 1994.
  16. T. Tjahjowidodo, F. Al-Bender, and H. Van Brussel, “Experimental dynamic identification of backlash using skeleton methods,” Mechanical systems and signal processing, vol. 21, no. 2, pp. 959–972, 2007.
  17. K. Worden, Nonlinearity in structural dynamics: detection, identification and modelling. CRC Press, 2019