Investigation of discrepancies in isotropic material and structural properties in lattice frameworks
Main Article Content
Abstract
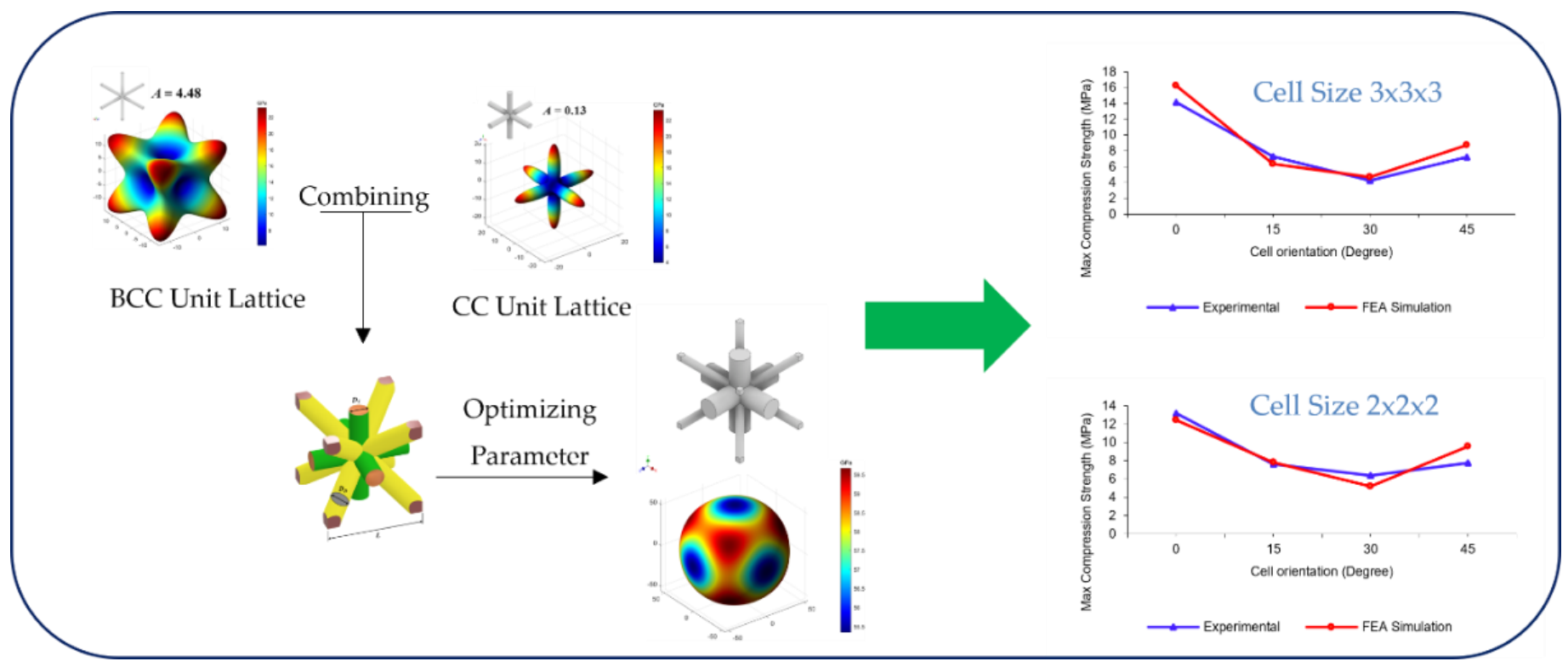
Lattice structures have developed as a vital component in advanced engineering applications due to their superior strength-to-weight ratios and adjustable mechanical properties. This paper focuses on examining the correlation between the isotropic features of lattices at the material level and their structural performance. The research used near-isotropic Crossing-cylinder (CC)- Body Centered Cubic (BCC) cells in various orientations and sizes. Both experimental analysis and finite element analysis were used to examine the compressive strength of the structure in each orientation. The results reveal that cell orientation is important for determining failure modes and mechanical performance at the structural level. At 0°, the lattice has higher compressive strength and energy absorption due to effective load transfer via CC-aligned struts. In contrast, higher orientations (e.g., 15°, 30°, and 45°) are dominated by collapse-type failures, indicating anisotropic behavior in an otherwise isotropic design. Smaller cell sizes have more strength at lower orientations due to their higher relative density, but larger cells perform better at higher orientations.
Downloads
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
References
[2] G. P. Borikar, A. R. Patil, and S. B. Kolekar, Additively Manufactured Lattice Structures and Materials: Present Progress and Future Scope, vol. 24, no. 11. Korean Society for Precision Engineering, 2023. doi: 10.1007/s12541-023-00848-x.
[3] Y. Li, D. Jiang, R. Zhao, X. Wang, L. Wang, and L. C. Zhang, “High Mechanical Performance of Lattice Structures Fabricated by Additive Manufacturing,” Metals (Basel), vol. 14, no. 10, 2024, doi: 10.3390/met14101165.
[4] H. Gharehbaghi, A. Farrokhabadi, and Z. Noroozi, “Introducing a new hybrid surface strut-based lattice structure with enhanced energy absorption capacity,” Mechanics of Advanced Materials and Structures, vol. 31, no. 14, pp. 2955–2964, 2024, doi: 10.1080/15376494.2023.2167246.
[5] A. Ahmad, L. Belluomo, M. Bici, and F. Campana, “Bird’s Eye View on Lattice Structures: Design Issues and Applications for Best Practices in Mechanical Design,” Metals (Basel), vol. 13, no. 10, 2023, doi: 10.3390/met13101666.
[6] K. M. Park, K. S. Min, and Y. S. Roh, “Design Optimization of Lattice Structures under Compression: Study of Unit Cell Types and Cell Arrangements,” Materials, vol. 15, no. 1, 2022, doi: 10.3390/ma15010097.
[7] Y. Lin et al., “Influence of Density Gradient on the Compression of Functionally Graded BCC Lattice Structure,” Materials, vol. 16, no. 2, 2023, doi: 10.3390/ma16020520.
[8] Z. Luo et al., “Effect of aspect ratio on mechanical anisotropy of lattice structures,” Int J Mech Sci, vol. 270, no. February, p. 109111, 2024, doi: 10.1016/j.ijmecsci.2024.109111.
[9] U. Hossain, S. Ghouse, K. Nai, and J. R. Jeffers, “Controlling and testing anisotropy in additively manufactured stochastic structures,” Addit Manuf, vol. 39, no. January, p. 101849, 2021, doi: 10.1016/j.addma.2021.101849.
[10] X. Chen et al., “A class of elastic isotropic plate lattice materials with near-isotropic yield stress,” Acta Mater, vol. 276, no. June, p. 120085, 2024, doi: 10.1016/j.actamat.2024.120085.
[11] H. Yin and C. Liu, “Anisotropy and Asymmetry of the Elastic Tensor of Lattice Materials,” J Elast, vol. 154, no. 5, pp. 659–691, 2023, doi: 10.1007/s10659-023-10028-7.
[12] D. Molavitabrizi and S. M. Mousavi, “Elasticity of Anisotropic Low-Density Lattice Materials,” Journal of Engineering Materials and Technology, Transactions of the ASME, vol. 143, no. 2, 2021, doi: 10.1115/1.4048931.
[13] G. P. Steven, “Homogenization of multicomponent composite orthotropic materials using FEA,” Commun Numer Methods Eng, vol. 13, no. 7, pp. 517–531, 1997.
[14] S. Daynes, “Isotropic cellular structure design strategies based on triply periodic minimal surfaces,” Addit Manuf, vol. 81, no. January, p. 104010, 2024, doi: 10.1016/j.addma.2024.104010.
[15] S. Xu, J. Shen, S. Zhou, X. Huang, and Y. M. Xie, “Design of lattice structures with controlled anisotropy,” Mater Des, vol. 93, pp. 443–447, 2016, doi: 10.1016/j.matdes.2016.01.007.
[16] J. Feng, B. Liu, Z. Lin, and J. Fu, “Isotropic octet-truss lattice structure design and anisotropy control strategies for implant application,” Mater Des, vol. 203, p. 109595, 2021, doi: 10.1016/j.matdes.2021.109595.
[17] G. Dong, Y. Tang, and Y. F. Zhao, “A 149 Line Homogenization Code for Three-Dimensional Cellular Materials Written in MATLAB,” Journal of Engineering Materials and Technology, Transactions of the ASME, vol. 141, no. 1, pp. 1–11, 2019, doi: 10.1115/1.4040555.
[18] A. A. Arifin, I. M. L. Batan, M. Bici, A. Wahjudi, and A. S. Pramono, “Isotropic Body-Centered Cubic (BCC) Lattice Structure Design,” in Smart Innovation in Mechanical Engineering, A. El Kharbachi, I. D. Wijayanti, P. Suwarta, and I. Tolj, Eds., Singapore: Springer Nature Singapore, 2025, pp. 45–53.
[19] A. Kumar, L. Collini, A. Daurel, and J. Y. Jeng, “Design and additive manufacturing of closed cells from supportless lattice structure,” Addit Manuf, vol. 33, no. January, p. 101168, 2020, doi: 10.1016/j.addma.2020.101168.
[20] R. Ismail, M. A. Nursafitri, A. P. Fardinansyah, and D. Fajar, “Design , fabrication , and performance testing of an energy storage and return ( ESAR ) foot prosthesis made of prepreg carbon composite,” vol. 5, no. 1, 2025.
[21] Z. Fang, Y. Ding, Y. Jiang, Y. Zheng, Z. Wang, and F. Zhou, “Failure mode analysis of stiffness-guided lattice structures under quasi-static and dynamic compressions,” Compos Struct, vol. 275, no. July, p. 114414, 2021, doi: 10.1016/j.compstruct.2021.114414.
[22] Z. Wang, X. Jiang, G. Yang, B. Song, and H. Sha, “Design and mechanical performance analysis of T-BCC lattice structures,” Journal of Materials Research and Technology, vol. 32, no. June, pp. 1538–1551, 2024, doi: 10.1016/j.jmrt.2024.08.021.
[23] I. C. Scheperboer, A. S. J. Suiker, R. A. Luimes, E. Bosco, and A. J. M. Jorissen, “Collapse response of two-dimensional cellular solids by plasticity and cracking: application to wood,” Int J Fract, vol. 219, no. 2, pp. 221–244, 2019, doi: 10.1007/s10704-019-00392-8.
[24] N. Li, S. Pang, S. Chen, Y. Liu, W. Aiyiti, and Z. Chen, “Design and application of hybrid lattice metamaterial structures with high energy absorption and compressive resistance,” Journal of Materials Research and Technology, vol. 33, no. September, pp. 7100–7112, 2024, doi: 10.1016/j.jmrt.2024.11.113.
[25] L. Zhang et al., “Energy absorption characteristics of metallic triply periodic minimal surface sheet structures under compressive loading,” Addit Manuf, vol. 23, no. July, pp. 505–515, 2018, doi: 10.1016/j.addma.2018.08.007.
[26] X. Ma, N. Zhang, Y. Chang, and X. Tian, “Multi-step deformation lattice structures from the rotation of unit cell,” Int J Solids Struct, vol. 288, no. November 2023, p. 112599, 2024, doi: 10.1016/j.ijsolstr.2023.112599.
[27] S. E. Alkhatib, A. Karrech, and T. B. Sercombe, “Isotropic energy absorption of topology optimized lattice structure,” Thin-Walled Structures, vol. 182, no. June 2022, p. 110220, 2023, doi: 10.1016/j.tws.2022.110220.
[28] S. Wang, Y. Zhu, J. Yu, L. Wang, and Z. Zheng, “Anisotropic mechanics of cell-elongated structures: Finite element study based on a 3D cellular model,” Thin-Walled Structures, vol. 205, no. PA, p. 112405, 2024, doi: 10.1016/j.tws.2024.112405.
[29] T. Tancogne-Dejean and D. Mohr, “Elastically-isotropic truss lattice materials of reduced plastic anisotropy,” Int J Solids Struct, vol. 138, pp. 24–39, 2018, doi: 10.1016/j.ijsolstr.2017.12.025.
[30] A. Kumar, L. Collini, A. Daurel, and J. Y. Jeng, “Design and additive manufacturing of closed cells from supportless lattice structure,” Addit Manuf, vol. 33, no. January, p. 101168, 2020, doi: 10.1016/j.addma.2020.101168.
[31] T. Yu et al., “Truss and plate hybrid lattice structures: Simulation and experimental investigations of isotropy, large-strain deformation, and mechanisms,” Mater Today Commun, vol. 35, p. 106344, 2023, doi: https://doi.org/10.1016/j.mtcomm.2023.106344.
[32] K. Snodderly, A. Cunningham, N. Zipin, M. K. Sung, M. Di Prima, and D. Porter, “Effect of lattice orientation on compressive properties of selective laser sintered nylon lattice coupons,” Mechanics of Materials, vol. 183, no. April, p. 104686, 2023, doi: 10.1016/j.mechmat.2023.104686.
[33] Y. Huang, A. R. O. Wan, K. Schmidt, P. Sefont, S. Singamneni, and Z. W. Chen, “Effects of cell orientation on compressive behaviour of electron beam powder bed fusion Ti6Al4V lattice structures,” Mater Today Proc, no. xxxx, pp. 0–4, 2023, doi: 10.1016/j.matpr.2023.04.522.
[34] X. M. Delgado and C. G. Merrett, “Examination of isotropy assumption in isogrid structures through analysis and experimentation on four isogrid variations,” Acta Astronaut, vol. 202, no. October 2022, pp. 422–432, 2023, doi: 10.1016/j.actaastro.2022.10.040.
[35] P. Li, F. Yang, Y. Bian, S. Zhang, and L. Wang, “Designable mechanical properties of modified body-centered cubic lattice materials,” Compos Struct, vol. 317, no. April, 2023, doi: 10.1016/j.compstruct.2023.117060.